

III) La déformation de l'Espace-Temps
1) La représentation de la déformation l'Espace-Temps
Tout corps déforme l'espace-temps qui l'entoure avec une courbure proportionnelle à sa masse. Il existe un exemple très célèbre permettant de se représenter ce phénomène : prenons un drap tendu, représentant l'espace-temps. Déposons une boule de pétanque : le drap se déforme sous le poids de la boule, et tout corps qui se déplacera à proximité sera attiré et tombera dans le trou créé par la boule. Plus la boule est lourde, plus le trou est profond. Dans le cas d'un trou noir, la "boule" a une masse telle que le trou est une véritable déchirure dans l'espace-temps, qui attire tout, même la lumière, bien qu'elle ait une masse infinitésimale.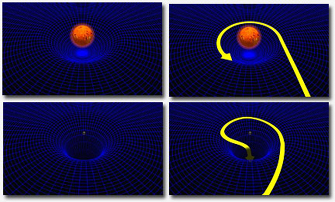
L'espace-temps représenté par le drap, se courbe sous le poids de la boule. Tout corps qui se déplace à côté de la boule est attiré par cette dernière et tombe dans le trou qu'elle a créé. Une dépression au sein du drap est formée.
2) La vitesse de libération.
La vitesse de libération est celle nécessaire pour se libérer de la force de gravité d'une planète. Elle est donnée par la relation : |
où G est la constante gravitationnelle : 6,67.10-11 N.m2.kg-2, avec v en m.s-1, M en kg et R en m.
Calcul de la vitesse de libération du Soleil :
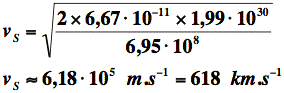 |
Calcul de la vitesse de libération de la Terre :
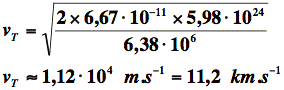 |
Schéma de la vitesse de libération de la Terre :
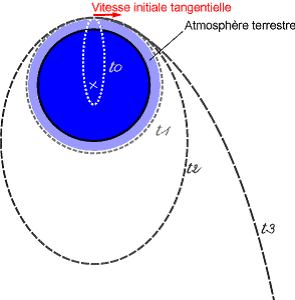
- v > 8 km.s-1 : la trajectoire est circulaire et ne heurte plus la Terre (trajectoire T1)
- v < 8 km.s-1 : la vitesse est insuffisante et l'objet retombe sur Terre (trajectoire T0)
- 8 km.s-1 < v < 11 km.s-1 : la trajectoire est une ellipse dont le périgée correspond au point de lancement (trajectoire T2 fermée)
- v > 11 km.s-1 : la trajectoire n'est plus fermée ; le mobile va s'éloigner à l'infini sur une trajectoire hyperbolique
Dans le cas d'un trou noir, la vitesse de libération est supérieure à la vitesse de la lumière, ce qui, d'après la relativité générale d'Einstein, est impossible. Ceci démontre qu'aucun corps, quel qu'il soit, ne peut s'échapper d'un trou noir. La lumière non plus, d'où le nom "trou noir", car c'est un corps noir parfait : il absorbe toutes les radiations et n'en émet aucune.
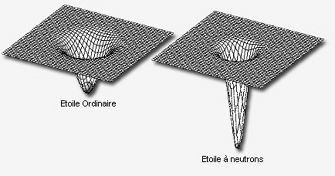
La théorie de la relativité générale d'Einstein décrit la gravitation comme une courbure de l'espace-temps. Plus la masse est concentrée, plus cette courbure est prononcée. Hors une étoile à neutrons est plus lourde qu'une étoile ordinaire, bien qu'elle soit plus petite. Plus une étoile est petite, plus sa masse augmente car la gravitation finit par l'emporter sur la pression de dégénérescence (force qui permet à une naine blanche ou une étoile à neutrons de ne pas s'effondrer sur elle-même malgré la gravitation) et donc plus le trou est profond.
3) Le rayon de Schwarzschild
L'horizon des évènements (le point de non-retour) est la limite à partir de laquelle la lumière ne peut plus s'échapper. Son rayon qui est le rayon de Schwarzschild, détermine le rayon que le corps doit avoir pour pouvoir retenir la lumière.Il peut être calculé pour tout corps, même le nôtre. Car n'importe quel corps peut devenir un trou noir : il suffit que son rayon soit inférieur ou égal au rayon de Schwarzschild, donné par la relation :
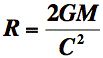 |
où G est la constante gravitationnelle : 6,67.10-11 N.m2.kg-2, C la vitesse de la lumière : 3,00.108 m.s-1,avec R en m et M la masse du corps en kg.
Démonstration :
Si la vitesse de libération est supérieure ou égale à la vitesse de la lumière :
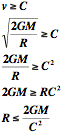 |
Calcul du rayon de Schwarzschild du Soleil :
 |
Calcul du rayon de Schwarzschild de la Terre :
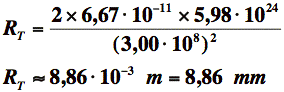 |
Ainsi, pour que le Soleil puisse retenir la lumière par son attraction gravitationnelle, il faudrait que son rayon soit inférieur ou égal à 2,95 km. Quant à la Terre, son rayon ne devrait pas dépasser les 8,86 mm. De telles compressions sont bien sûr impossibles.
4) Le paramètre gravitationnel
On appelle "paramètre gravitationnel" le rapport du rayon de Schwarzschild sur le rayon réel :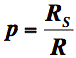 |
Ce paramètre est très inférieur à 1 pour les objets courants, et est proportionnel à la densité de l'objet.
Le paramètre gravitationnel d'un trou noir est donc supérieur à 1.
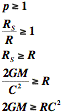 |
En remplaçant G et C par leurs ordres de grandeur :
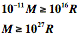 |
En effet : il faudrait que la masse en kg d'une planète soit au moins 1027 fois plus grande que son rayon pour qu'elle retienne la lumière.
I) Définition et Formation
1) Que sont-ils?
2) D'où viennent-ils?
3) Comment se forment-ils?
4) Comment est-ce structuré?
5) Hypothèses
II) L'Espace-Temps
1) Qu'est-ce?
2) Einstein: Le mélange espace/temps
3) Distorsion de l'E.T.
4) Schwarzschild et Kerr : Influence sur l'E.T.
III) Déformation de l'E.T.
1) Représentation
2) Vitesse de libération
3) Rayon de Schwarzschild
4) Paramètre gravitationnel
Conclusion